Artículo de Investigación

 

Concepciones de los docentes sobre las competencias matemáticas

Teachers’ conceptions of mathematical skills

Concepções de professores sobre habilidades matemáticas

 

*YennY Paola ladino Bonilla

 

*Candidata a doctora en Ciencias de la Educación Universidad Arturo Prat de Chile; Magister en Ciencias de la Educación con énfasis en Didáctica de las Matemáticas; Especialista en Pedagogía; Licenciada en Matemáticas y Física. Docente de aula en el área de matemáticas en secundaria y media académica. ORCID https://orcid.org/0000-0002-0104-1096

 

DOI: https://doi.org/10.18634/sophiaj. 19v.1i.1213

 

Información del artículo

 

Recibido: julio de 2022 Revisado: septiembre de 2022 Aceptado: noviembre de 2022 Publicado: enero - junio 2023

 

Palabras clave: competencias matemáticas, concepciones de los docentes, educación matemática, enseñanza de las matemáticas, percepciones docentes

 

Keywords: mathematical skills, teachers’ conceptions, mathematics education, mathematics teaching, teacher perceptions.

 

Palavras-chave: habilidades matemáticas, concepções de professores, educação matemática, ensino de matemática, percepções de professores

 

Cómo citar: /how cite:

Ladino Bonilla, Y. P. (2023). Concepciones de los docentes sobre las competencias matemáticas. Sophia, 19(1). https://doi. org/10.18634/sophiaj.19v.1i.1213

Sophia-Educación, volumen 19 número 1. Enero/junio 2023. Versión español

 

Correspondencia de autor:

 

yennypl@iemjoseustasiorivera.edu.co

Resumen

La investigación describe las concepciones de los docentes sobre las competencias en matemáticas como reguladoras en la calidad de la educación en las diferentes Instituciones Educativas de Florencia, Colombia. En consonancia con lo anterior, el fin del presente documento es la caracterización de las concepciones de las competencias matemáticas de los docentes del municipio de Florencia enfocadas a los contenidos curriculares, didácticos y de evaluación del aprendizaje, para identificar si existen diferencias significativas entre las categorías emergentes en relación a su función, capacidad y desempeño de su aplicabilidad por parte de los docentes. Dada la naturaleza mixta de la indagación, se opta por un alcance descriptivo donde se expongan las situaciones, costumbres y actitudes del profesorado ante las variables dependientes e independientes de la muestra. Los datos se recogieron a través de la implementación de encuestas estructuradas a 73 docentes de matemáticas, las cuales fueron analizadas por el índice de varianza ANOVA del programa Statistical Package for the Social Sciences, encontrando multifactorialidad en las concepciones al identificar y describir 16 categorías emergentes relacionadas con el pensamiento matemático, trabajo en el aula e instrumentos de evaluación de los contenidos, resultando el Aprendizaje Significativo Socio Cultural el de mayor prevalencia. Por lo anterior, la investigación es una descripción estratégica de cara a la realidad del saber docente sobre la implementación  de los componentes educativos (competencias) descritos por el Ministerio de Educación Nacional.

Abstract

 

This research describes the teachers’ conceptions about the competences in mathematics as regulators in the quality of education in the different Educational Institutions in Caquetá. That is why the purpose of this document is the characterization of the conceptions of math competences in teachers from the municipality of Florencia focused on the curricular contents, didactic and learning assessment to identify if there are significant differences between the emerging categories in relation to their function, capacity and performance of their applicability by the teachers. Due to the mixed nature of the inquiry, a scope is chosen where teacher’s situations, customs and attitudes are described in face of the dependent and independent variables of the sample. The data was collected through the implementation of structured surveys to 73 mathematics teachers which were analyzed by the ANOVA variance index from the Statistical Package for the Social Sciences program; finding multifactoriality in the conceptions when identifying and describing 16 emerging categories related to mathematical thinking, classroom work and content assessment instruments, resulting in the Significant Sociocultural Learning the most prevalence. Due to the above, the research is a strategic description for the reality of teaching knowledge about the implementation of educational components (competencies) described by the Ministry of National Education.

 

RESUMO

 

A pesquisa descreve as concepções dos professores sobre as competências em matemática como reguladores da qualidade da educação nas diferentes Instituições Educativas de Florencia, Colômbia. Em consonância com o exposto, o objetivo deste documento é a caracterização das concepções das competências matemáticas dos professores do município de Florença com foco nos conteúdos curriculares, didáticos e de avaliação de aprendizagem, para identificar se existem diferenças significativas entre as categorias .emergindo em relação à sua função, capacidade e desempenho de sua aplicabilidade pelos professores. Dado o carácter misto do inquérito, optou-se por um âmbito descritivo onde as situações, costumes e atitudes do corpo docente são expostas às variáveis dependentes e independentes da amostra. Os dados foram recolhidos através da aplicação de inquéritos estruturados a 73 professores de matemática, os quais foram analisados pelo índice de variância ANOVA do programa Statistical Package for the Social Sciences, encontrando multifatorialidade nas concepções ao identificar e descrever 16 categorias emergentes relacionadas. , trabalhos de sala de aula e instrumentos de avaliação de conteúdo, sendo a Aprendizagem Sociocultural Significativa a mais prevalente. Portanto, a pesquisa é uma descrição estratégica voltada para a realidade do conhecimento docente sobre a implementação dos componentes educacionais (competências) descritos pelo Ministério da Educação Nacional.

Introducción

La presente investigación se desarrolla en la ciudad de Florencia, departamento de Caquetá, al sur de Colombia, esta ciudad se caracteriza por estar dentro de la región amazónica, se le conoce por tener zonas elevadas en flora, fauna y ser una zona trófica representativa en bosques, la mayoría de sus habitantes son descendientes indígenas y está conformada por 110.000 habitantes aproximadamente, sin embargo, los docentes son de todas las regiones del país debido a la necesidad del servicio y el método de selección por concurso a las vacantes existentes, también, porque tiene la única universidad pública del sector, la Universidad de la Amazonia .

Se circunscribe en el área de las matemáticas en el sector estatal del país, y dada la importancia que tienen las competencias matemáticas y las concepciones que tienen los docentes de las mismas en el desarrollo de los aprendizajes, el documento está orientado a describir información específica sobre las concepciones de las competencias matemáticas en un grupo de docentes de educación media en Florencia (Caquetá). Para esto se realizó una revisión documental con el propósito de crear un marco teórico relacionado con competencias matemáticas en contenidos curriculares, enfoque didáctico y en la evaluación del aprendizaje. En este sentido, la justificación del trabajo se basa en la necesidad de generar información sobre el tema de estudio, debido a las escasas investigaciones relacionadas con las concepciones matemáticas. Adicionalmente la revisión permite llevar a cabo una metodología descriptiva, mixta con un muestreo aleatorio simple en la descripción de las concepciones de los docentes sobre las competencias matemáticas.

El objetivo general se orienta a caracterizar las concepciones de las competencias matemáticas en docentes del municipio de Florencia, teniendo en cuenta contenidos curriculares, didáctica y evaluación. Para lograrlo, se establecieron tres objetivos específicos: describir las concepciones de docentes sobre competencias matemáticas en los contenidos curriculares que se orientan en clase, en enfoques didácticos aplicados por ellos, y en evaluación que realizan del aprendizaje. Por último, la pregunta de investigación se expresa de la siguiente manera: ¿Cuáles son las concepciones sobre competencias matemáticas que tienen los docentes de las Instituciones Educativas de Florencia? Los resultados confirman que, aunque las competencias matemáticas obtuvieron valores relativamente bajos en su nivel de significancia, solo el Aprendizaje Significativo Socio Cultural (ASSC) representó una diferencia estadísticamente significativa.

 

Marco teórico

Concepciones sobre las competencias matemáticas Por disposición del Estado, le compete al Ministerio de Educación Nacional la solución de las necesidades insatisfechas, entre las cuales se identifica la falta de una educación de calidad, como lo estipula la Ley 115 de 1994 o la Ley General de Educación, proponiendo una transformación curricular de todas las clases enfocadas al mejoramiento de la misma educación. Según el informe de la Organización para la Cooperación y el Desarrollo Económico (OCDE), Colombia está entre los diez países con más estudiantes con bajo rendimiento escolar en matemáticas, debido a la carencia de políticas institucionales que fortalezcan las competencias en el área, tanto en básica primaria, media vocacional y estudios superiores.

Por lo anterior, el rendimiento académico hace referencia al nivel de éxito que un estudiante logra en su desempeño educativo relacionados con los objetivos de aprendizaje, los cuales son evaluados a través de métodos estandarizados (proyectos, exámenes o calificaciones) (Grasso, 2020). De igual forma, el rendimiento académico se relaciona con la calidad de la educación básicamente en dos aspectos, el primero hace hincapié en que una educación de calidad debe caracterizarse por tener un cuerpo docente capacitados, recursos educativos óptimos, programas curriculares relevantes, una gestión eficiente del sistema educativo y un entorno de aprendizaje favorable. El segundo aspecto describe el rendimiento académico de los estudiantes al adquirir las habilidades, conocimientos y competencias que se espera que desarrollen en su proceso educativo.

Esta relación entre el rendimiento académico y la calidad de la educación, puede proporcionarles a los estudiantes las herramientas necesarias para obtener logros académicos al igual que su motivación en áreas como las matemáticas, sin embargo, estudios realizados por Méndez, et. al. (2018) de la Facultad de Ciencias de la Educación de la Universidad de la Amazonia, señalan que el aprendizaje de las matemáticas en el Caquetá no es el mejor:

los estudios aseguran que, en la educación básica y media, no desarrollan las habilidades necesarias que les permitan tener un conocimiento básico en el manejo de los conceptos matemáticos y aplicativos, razón por la cual no pueden desarrollar soluciones matemáticas de mayor nivel académico, como es el caso de los vistos en la universidad. (p.2)

 

Otras investigaciones como la de Ramírez (2016) concuerdan con las descritas por Méndez et al. (2018) sobre la perspectiva del nivel educativo de la educación media hacia la formación superior en el sur del país:

A un mayor nivel de aplicación adecuada de las matemáticas, mayores serán los aciertos de los futuros profesionales, que contarán con herramientas que le posibilitará el triunfo personal y del país en general, colocando a la nación en un acorde crecimiento de sus recursos económicos, naturales, sociales, políticos y humanos, que se encargarán a su vez de generar crecimiento en todos los aspectos del país. (p.33)

 

Estos trabajos investigativos sobre la calidad de la educación en el área de matemáticas, se ven fundamentados en la necesidad de describir y analizar procesos en el trabajo docente, por lo tanto, ha sido necesario mencionar el tema de las concepciones, no sin aclarar que existen pocas investigaciones que abarcan el análisis de las concepciones de los docentes sobre las competencias matemáticas tanto a nivel nacional como internacional, por lo que todavía no hay una unidad de criterio sobre estas (Pareja y Martínez, 2008).

La definición de las concepciones que se emplea en la presente investigación, se basa en las premisas de Moreno y Azcárate (2003), descritas de la siguiente manera:

las concepciones son organizadores implícitos de los conceptos, de naturaleza esencialmente cognitiva y que incluyen creencias, significados, conceptos, proposiciones, reglas, imágenes mentales, preferencias, etc., que influyen en lo que se percibe y en los procesos de razonamiento que se realizan. (p.267)

 

De igual forma Brousseau (2007), destaca su concepto sobre concepciones en relación a que son estructuras cognitivas que los estudiantes construyen para comprender e interpretar los conceptos matemáticos, las cuales son desarrolladas por medio de las interacciones del estudiante con otros individuos (profesores y estudiantes) y el medio ambiente.

Desde los referentes anteriores, se describieron las concepciones sobre las competencias matemáticas, permitiendo que los docentes aborden un desarrollo crítico de la enseñanza de las matemáticas. En estas condiciones, González (2008) describe estas competencias como una forma interna que privilegia el dominio de la disciplina con el propósito de estructurarse a sí misma, por lo tanto, esto hace referencia al desarrollo de las competencias de matemáticas en contenidos curriculares, enfoque didáctico y la evaluación del aprendizaje (Figura 1) (Becerra, 2017; Listón y Zeichner, 1993).

Figura 1 .Funcionalidad de las Concepciones de los Docentes sobre las Competencias Matemáticas

Fuente: Autoría propia

Según las investigaciones de Becerra (2017); Listón y Zeichner (1993); Pareja y Martínez (2008), se explican las concepciones de los docentes sobre las competencias matemáticas en contenidos curriculares, enfoque didáctico y evaluación del aprendizaje.

Concepciones de los docentes sobre competencias matemáticas en contenidos curriculares (COMCC). Las COMCC hacen referencia a: 1. Aprendizaje y cognición (AC); 2. Dominio Conceptual Disciplinar (DCD); 3. Trasferencia de Conocimientos (TC); 4. Enseñanza (E) y 5. Aprendizaje Significativo Socio Cultural (ASSC).

Se caracterizan por orientar al estudiante hacia diferentes vías de solución, alcanzando la autoevaluación de su rendimiento en un desarrollo cognitivo del aprendizaje (Resnick, 1996).

Concepciones de los docentes sobre competencias matemáticas en el enfoque didáctico (CDCMED). el enfoque didáctico desarrolla diferentes categorías emergentes, como es el caso del constructivismo social (C.S) descrito por Gregorio (2002) como las actividades diarias en el aula de clase. El segundo enfoque emergente es el fenomenológico (EF), el cual relaciona los problemas que afrontan los docentes de matemáticas en alcanzar un aprendizaje significativo por parte del estudiantado. Este aprendizaje por lo regular es basado en los contextos disciplinares específicos y en la solución de problemas de la vida cotidiana (véanse los aportes de Radford, 2013; Freudentha,1983; y Puig, 1997).

El tercer enfoque es el Semiótico (ES); este controla y “analiza la cultura matemática, entendida como un proceso de culturización matemática, y se distinguen y analizan los tres aspectos esenciales que la caracterizan como disciplina científica: el campo conceptual, la fenomenología y la funcionalidad” (Socas, 2012, p.1). El último es el del Enfoque Antropológico (EA), el cual se caracteriza por la “focalización en las determinaciones sociales de los fenómenos indagados, su pauta de análisis de las culturas humanas basada en el modelo praxeológico, su enfoque institucional y epistemológico a la enseñanza” (Castela, 2017, p.8).

Concepciones de los docentes sobre competencias matemáticas en la evaluación del aprendizaje (CPMEA). Las CPMEA posee siete categorías emergentes: 1. Evaluación del Proceso del Rendimiento (EPR); 2. Evaluación en el Proceso de Desarrollo de Aptitudes (EPDA); 3. Evaluación de la Dimensión Valorativa (EDV); 4. Evaluación de la Dimensión Teórica (EDT); 5. Evaluación Integral (EI); 6. Evaluación en el Proceso de Desempeño (EPD); y 7. Evaluación en la Dimensión Practica (EDP).

El fin de la evaluación debe ser siempre el de ayudar al estudiante a aprender, por lo tanto es de vital importancia describir los aspectos generales de estos enfoques, Diaz, et. al. (2003) describen que: “los mecanismos mediante los cuales se participa en la evaluación son variados, involucran la actividad individual y colectiva (p.2) (véanse igualmente Serrano de Moreno, 2002; Nieto, et. al., 2003). Por lo tanto, las competencias se transformaron en habilidades eficientes a partir de las cuales las matemáticas solucionan conflictos pedagógicos en los que los docentes utilizan modelos matemáticos tradicionales, lo que produciría según Prieto y Contreras (2008) un cambio del conocimiento disciplinario en relación a las Competencias Matemáticas basadas en su evaluación:

si se acepta que las prácticas evaluativas no son procesos meramente técnicos ni de control, es necesario cumplir con una serie de requisitos para que sus resultados reflejen efectivamente los aprendizajes de los estudiantes y el desarrollo de las respectivas habilidades. Ello implica que el profesor realice un complejo proceso de transformación del conocimiento disciplinario para su presentación didáctica, de manera de facilitar su comprensión por parte de los estudiantes; que defina los criterios de evaluación, diseñe instrumentos evaluativos en consonancia con lo anterior y determine cómo va a comunicar y trabajar sus resultados, articulando contenido disciplinario, su didáctica y la forma de evaluarlo. (p. 255)

 

 

Metodología

Enfoque metodológico

La investigación posee un enfoque mixto, debido a que analiza datos cualitativos y cuantitativos simultáneamente para responder al planteamiento del problema. El alcance es descriptivo, puesto que busca identificar situaciones, costumbres y actitudes de los docentes y sus relaciones con las variables de estudio (Van Dalen y Meyer, 2006).

El diseño es no experimental, “pues observa los fenómenos tal como se dan en el contexto natural y posteriormente los analiza, es decir no se manipulan deliberadamente las variables, no se construye ninguna situación, solamente se observa la realidad ya existente sin intervención alguna” (Mello, 2017, p.6). El sistema de muestreo es probabilístico, debido a que el azar es la razón principal de selección, por lo que las reglas sistemáticas y

aleatorias rigen este tipo de sistema. A su vez esto permite que la muestra sea verdaderamente significativa en la población (Tamayo, 2004). El muestreo es aleatorio simple, cada docente de la población tiene la misma probabilidad de ser seleccionado para la muestra, no permite la influencia de factores externos que predispongan la selección objetiva de la muestra (Tamayo, 2004).

Categorías de análisis

La encuesta se utiliza para estudiar poblaciones mediante el análisis de muestras representativas a fin de explicar las variables de estudio y su frecuencia. Para la investigación se tuvieron en cuenta 13 preguntas centradas en la creación del conocimiento y es aquí donde se fundamentan tres categorías principales a identificar: Contenidos curriculares, enfoque didáctico y evaluación del aprendizaje en la concepción de competencias matemáticas. Es así que el entorno de mayor incertidumbre es el formado a partir del conocimiento individual de quienes lo conforman (Docentes) y construirlo a partir de la información y los datos recolectados en relación a las categorías emergentes basadas en la investigación de Pareja y Martínez (2008) (Tabla 1).

Tabla 1. Descripción de las variables de estudio

 

Fuente: (Pareja y Martínez, 2008)

 

Las respuestas de las encuestas están ordenadas, segmentadas, categorizadas y clasificadas, en forma iterada según metodología de Becerra (2017), en función de su afinidad semántica y sintáctica en relación a la categoría de competencias matemáticas (CPM).

Participantes

La población bajo estudio está constituida por 90 docentes del área de matemáticas en ejercicio en la educación media en Instituciones Educativas del sector público en la zona urbana del municipio de Florencia, departamento de Caquetá. El marco muestral utilizado es el registro del Dane (2018) y la Secretaría de Educación Departamental del Caquetá. El modelo muestral aplicado corresponde al cálculo a partir de una población conocida (finita), como se indica a continuación: , donde n: tamaño de la muestra requerido, N: población de 90 docentes, Z: coeficiente 1,96 correspondiente a un 95% de confianza, E: grado de error del 5% (0,05) e índices de variabilidad de respuesta P; Q: 50% (0,5).

Instrumentos de obtención de información

Como fuente de información primaria se utilizó la técnica de encuesta estructurada, aplicada directamente en el medio donde se presenta el fenómeno de estudio (muestra representativa de la población), con el fin de obtener ediciones cualitativas y cuantitativas de testimonios que ayudarían a confrontar la teoría con la práctica en la búsqueda de la verdad objetiva.

La encuesta utilizada está validada en el marco de la investigación “Concepciones sobre competencias matemáticas en docentes de educación básica, media y universitaria” de Pareja y Martínez (2008) y la aplicación del análisis de Alfa Crombach realizada por los especialistas en procesos metodológicos Perdomo y Vargas (comunicación personal, 4 de enero, 2018), los cuales establecieron un índice de confiabilidad de forma y contenido del 0,81 y 0,81 correspondientemente.

A su vez, el trabajo se basa en fuentes secundarias provenientes de tesis, artículos científicos, reflexiones por teóricos y demás documentos que fundamentan las concepciones de los docentes sobre las competencias en matemáticas.

Trabajo de campo

El trabajo de campo se desarrolló en tres fases metodológicas:

Fase de reflexión y preparación del proyecto. En esta primera fase se formuló el problema de investigación, para

luego seleccionar la estrategia metodológica en la identificación de la muestra, contextos y fechas.

Fase de realización del trabajo de campo. En este punto, se implementó la encuesta a los 73 docentes del área de matemática en 13 Instituciones Educativas del municipio de Florencia, a su vez, se ajustaron las técnicas de generación de información para su respectivo archivo y análisis preliminar.

Fase de análisis final y escritura. Esta última fase corresponde con el análisis de la información obtenida en la

realización del trabajo de campo y la redacción del informe final.

Análisis de datos

Con los resultados de las categorías emergentes, se estableció un estudio estadístico en relación al análisis de varianza ANOVA realizado en el programa Statistical Package for the Social Sciences (SPSS), el cual permitió contrastar la hipótesis nula de que las medias de N poblaciones (N>2) son iguales, frente a la hipótesis alternativa de que por lo menos una de las poblaciones difiere de las demás en cuanto a su valor esperado:

Ho: Las concepciones de las competencias matemáticas de los Contenidos Curriculares, Enfoque Didáctico y Evaluación del Aprendizaje no presentan diferencias significativas en su nivel de significancia basados en sus categorías emergentes entre los 73 docentes encuestados.

H₁: Las concepciones de las competencias matemáticas de los Contenidos Curriculares, Enfoque Didáctico y Evaluación del Aprendizaje presentan diferencias significativas en su nivel de significancia basados en sus categorías emergentes entre los 73 docentes encuestados.

Este contraste de las dos hipótesis, es importante comprobarlo para generar los resultados experimentales con respecto a la variable dependiente.

Resultados

Los resultados de las concepciones de los docentes sobre las competencias matemáticas, se delimitaron de acuerdo al recuento y análisis de opiniones de los docentes en tres temas o categorías: (a) Concepciones de los Docentes sobre las Competencias Matemáticas y Contenidos Curriculares (CDCMCC; (b) Concepciones de los Docentes sobre las Competencias Matemáticas y Didáctica (CDCMD); (c) Concepciones de los Docentes sobre las Competencias Matemáticas y Evaluación (CDCME).

a.       Concepciones de competencias matemáticas y contenidos curriculares

La figura 1 representa la prevalencia de las categorías emergentes que surgen de los siete interrogantes relacionados con los contenidos curriculares de las matemáticas, establecidos por el pensamiento numérico, métrico, espacial, aleatorio y variacional.

Figura 2. Prevalencia de categorías emergentes sobre concepciones de competencias matemáticas y contenidos curriculares

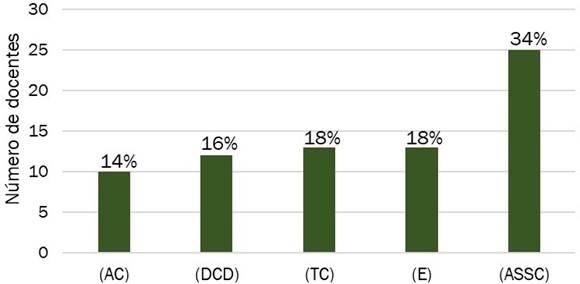
Fuente: autoría propia

 

Básicamente, la categoría emergente con el mayor porcentaje de la muestra es el Aprendizaje Significativo Socio Cultural (ASSC) con el 34 % de prevalencia, el segundo lugar lo comparten la Enseñanza (E) y la Trasferencia de Conocimientos (TC) con un 18 %, seguido del Dominio Conceptual Disciplinar (DCD) representado por el 16 %, por último y no menos importante, el 14 % de los docentes describe el Aprendizaje y Cognición (AC) de los contenidos curriculares.

b.                                          Concepciones de competencias matemáticas y didáctica

Dentro de la pregunta 9 y 10 de la encuesta estructurada, se identificaron cuatro (4) categorías emergentes relacionadas con las concepciones de competencias matemáticas y didáctica. Tales categorías, obtuvieron porcentajes de prevalencia diferenciables entre la muestra de estudio. El Enfoque Antropológico (EA) tuvo la más alta prevalencia con el 34 %, seguido del Enfoque Semiótico (ES) con un 27 %, Enfoque Fenomenológico (EF) con 22 % y por último el Constructivismo Social (C.S) con 18 % (Figura 3).

Figura 3. Prevalencia de categorías emergentes sobre las concepciones de competencias matemáticas y didáctica

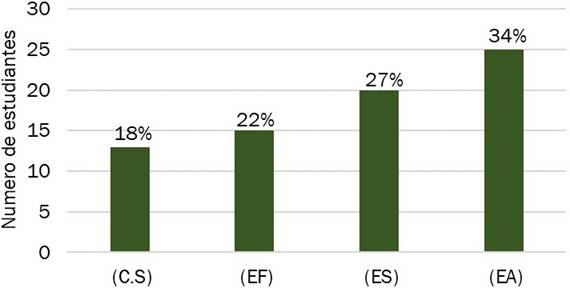
Fuente: autoría propia

c.               Concepciones de competencias matemáticas y su evaluación

Las concepciones de los 73 docentes sobre las competencias matemáticas y su evaluación, responden a siete categorías emergentes de las últimas tres preguntas de la encuesta. La Evaluación en la Dimensión Práctica (EDP) obtuvo la prevalencia más alta con el 20% de docentes, en segundo lugar, con un 15% se ubica la Evaluación en el Proceso de Desempeño (EPD), seguido de la Evaluación Integral (EI), Evaluación de la Dimensión Teórica (EDT) y Evaluación de la Dimensión Valorativa (EDV) con el 14% respectivamente. En cuarto lugar, la Evaluación en el Proceso de Desarrollo de Aptitudes (EPDA) corresponde al 12% y la prevalencia menos significativa con 11% perteneciente a la Evaluación del Proceso del Rendimiento (EPR) (Figura 4).

Figura 4. Prevalencia de categorías emergentes sobre las concepciones de competencias matemáticas y su evaluación.

 

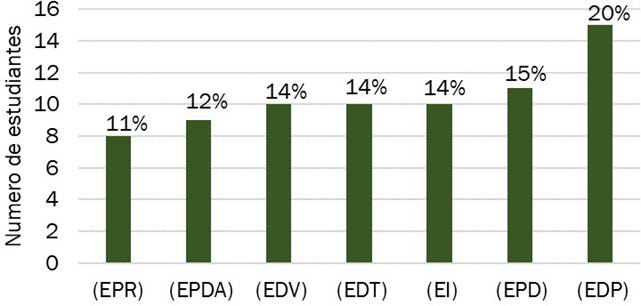
Fuente: autoría propia

 

Es claro que las 16 categorías emergentes distribuidas en los Contenidos Curriculares (CPMCC), Enfoque Didáctico (CPMED) y la Evaluación del Aprendizaje (CPMEA) poseen porcentajes de prevalencia similares en su nivel de significancia. Es de vital importancia identificar cuáles presentan diferencias realmente significativas, para así establecer cuáles categorías son las que los docentes contextualizan, conocen, manejan e integran las concepciones que tienen los docentes sobre las competencias matemáticas. Para ello se implementó el análisis de varianza de un factor denominado ANOVA como se muestra en la Tabla 2 y 3.

ANOVA calcula varias sumas de cuadrados para analizar la variabilidad general de los datos, así como la variabilidad dentro y entre grupos. A partir de estas sumas de cuadrados, se puede obtener la media y la varianza correspondientes. Para calcular la suma, se debe de tener en cuenta los siguientes conceptos:

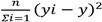Suma de cuadrados (SCT). Esta es la suma de las diferencias al cuadrado entre cada observación y la media total de todos los grupos. Se calcula sumando los cuadrados de las desviaciones de cada valor de la media global como lo indica la fórmula: STC                                                  (Ott, et. al., 2019).

Suma de cuadrados entre grupos (SCG). Es la suma de los cuadrados de  la diferencia entre la media del grupo y la media general. Se calcula sumando los cuadrados de la diferencia entre la media de cada grupo y la media poblacional, ponderada por el tamaño de cada grupo: SCG 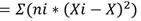 (Ott, et. al, 2019).

Suma de cuadrados dentro de grupos (SCD). Es la suma de las diferencias al cuadrado entre cada observación y la media del grupo respectivo. Se calcula sumando el cuadrado de la desviación de cada valor de la media de su grupo en cada grupo por separado y luego sumando estos valores en todos los grupos: SCD 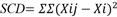 (Peña y Prieto 2005).

Una vez obtenida la suma de cuadrados, se puede calcular el promedio y la varianza:

Promedio. Para obtener el promedio, la suma correspondiente (SCT, SCG o SCD) se divide por el número correspondiente de grados de libertad. Los grados de libertad son una medida de la cantidad de información en los datos que se pueden usar para estimar un parámetro.

Varianza. La varianza se obtiene dividiendo la suma correspondiente (SCT, SCG o SCD) entre los grados de libertad correspondientes. La dispersión es una medida de la distribución de datos relativa a la media

Tabla 2. Resumen de las categorías emergentes

 

Fuente: Autoría propia

 

La Tabla 2 describe el resumen del promedio y varianza de las 16 categorías emergentes utilizadas para implementar el análisis de varianza en la Tabla 3. Al realizar el análisis de varianza, sew determinó que las Concepciones de competencias matemáticas y didáctica al igual que las Concepciones de competencias matemáticas y Evaluación no presentan diferencias en su nivel de significancia entre sus categorías emergentes, debido a que el índice de probabilidad descrito en la Tabla 3, es mayor al nivel de significancia de 0,05. En otras palabras, el índice de probabilidad de las competencias matemáticas y didáctica es 0,09 > 0,05 y el índice de probabilidad de las competencias matemáticas y evaluación es 0,07 > 0,05. En este caso se acepta la hipótesis nula “H₀”, la cual estipula que:

Las diferencias de los porcentajes de prevalencias de las categorías emergentes (CS); (DF); (ES) y (EA) que conforman el enfoque didáctico, al igual que la (EPR); (EPDA); (EDV); (EDT); (EI); (EPS) y (EDP) que constituyen la evaluación del aprendizaje, no presentan diferencias significativas entre las concepciones descritas por los 73 docentes encuestados (Tabla 2 y 3).

Tabla 3. Análisis de varianza de un factor

a. Concepciones de competencias matemáticas y contenidos curriculares

Fuente: Autoría propia

 

Caso contrario pasa con las Concepciones de competencias matemáticas y contenidos curriculares, donde el índice de probabilidad es menor que el de confianza, pues se tiene que: 0,01 < 0,05. Por lo anterior se rechaza H₀ y se acepta H₁: “las concepciones de las competencias matemáticas de los Contenidos Curriculares, presentan diferencias estadísticamente significativas al menos en un grupo de categorías emergentes entre los 73 docentes encuestados”.

Ahora, es importante identificar qué categoría emergente presenta tal diferencia, para ello, se aplica la Prueba de Tukey, la cual utiliza la diferencia honestamente significativa “HSD” determinada por el multiplicador (Valor de Qα= 3,12), el cuadrado del error medio (Mse= 0,15) y el tamaño de cada uno de los grupos (n= 73).

Por último, para terminar la Prueba de Tukey, el valor de HSD = 0,14 el cual es comparado con la media aritmética de cada uno de los grupos (categorías emergentes), donde se estipula que el Aprendizaje Significativo Socio Cultural (ASSC) posee la diferencia honestamente significativa, debido a que la diferencia de su media aritmética con los demás grupos es superior a la de HSD [(Aprendizaje Significativo Socio Cultural (ASSC) 0,34 – Enseñanza

(E) 0,17 = 0,17]; [(Aprendizaje Significativo Socio Cultural (ASSC) 0,34 - Trasferencia de Conocimientos (TC) (0.17)

= 0.17]; [(Aprendizaje Significativo Socio Cultural (ASSC) 0,34 - Dominio Conceptual Disciplinar (DCD) 0.16= 0,18]

y [(Aprendizaje Significativo Socio Cultural (ASSC) 0,34 - Aprendizaje y cognición (AC) 0.13= 0.21].

 

Discusión

Para determinar los resultados de la investigación en cada objetivo específico propuesto, se hace necesario dimensionar y contextualizar una serie de términos y definiciones que ayuden a comprender las categorías emergentes, para así establecer un análisis más claro de los enunciados descritos por los docentes encuestados. En primer lugar, se puede discutir sobre las Concepciones que tienen los docentes acerca de las competencias matemáticas enfocadas a la didáctica (CPMED) y su evaluación del aprendizaje (CPMEA), debido a que sus características emergentes no poseen una diferencia significativa entre sí.

Los docentes poseen Concepciones sobre las Competencias Matemáticas y la Didáctica, enfocadas al contexto cotidiano (con ejemplos de la vida diaria o ficticios), donde se posibilita la construcción de componentes y objetos matemáticos de su interés (Enfoque Antropológico) para que un individuo:

pueda en cada momento de su vida, desarrollar en pleno su índole humana, requiere de recursos social e históricamente producidos que se ubican fuera de él (…), por eso, lo Didáctico, es decir el conjunto de los fenómenos de difusión y apropiación de cualquier elemento de la cultura, representa la columna vertebral de lo Humano. (Castela 2017, p.9)

 

Con respecto a la interacción académica que el Enfoque Antropológico genera, es importante ver los aportes de Chevallard (1999).

A su vez, los docentes establecen que lo primordial es dar uso a conceptos y teorías matemáticas, a través de la resolución de problemas (Enfoque Semiótico), “a partir de la organización de los objetos de la matemática en campos conceptuales y de los estadios de desarrollo de los mismos” (Socas, 2012, p.1). Otro enfoque identificado fue el fenomenológico (EF), pues los docentes se orientan por una matemática lógica, debido a que estos son un mediador no de manera declarativa (Castro, 2011), en el mismo sentido Waldegg (1998) describe: “al atribuir al sujeto cognoscente el papel decisivo en la construcción del conocimiento, la hipótesis fenomenológica obliga, en cierto sentido, a tener en cuenta la intencionalidad o la finalidad del sujeto cognoscente” (p.20). El último enfoque emergente didáctico descrito es el constructivismo social (CS), que está orientado a las manifestaciones de importancia de la interacción social, “la enseñanza constructivista no se basa en diseñar ejercicios, sino en diseñar entornos sociales de aprendizaje y alfabetización matemáticas, de crear un aula compleja, emocionante y especulativa” (Gregorio, 2002, p.128).

El segundo grupo de categorías emergentes, relacionadas con las concepciones de competencias matemáticas de los docentes, enfocadas a la Evaluación del aprendizaje (CPMEA), tampoco obtuvo diferencias significativas entre sus categorías, ya que, el total de encuestados manifiesta que la importancia de la Evaluación en la Dimensión Práctica (EDP), radica en el uso del conocimiento matemático en la solución de problemas propios del área o demás ramas del saber; la Evaluación en el Proceso de Desempeño (EPD) es de vital importancia para el seguimiento del cumplimiento de los responsabilidades y funciones por parte de los alumnos en el proceso del aprendizaje matemático.

Del mismo modo, la Evaluación Integral (EI) es percibida como la implementación de estrategias de evaluación basadas en desempeños, debido a la necesidad de los estudiantes de demostrar sus actitudes, destrezas y conocimientos en el desarrollo de actividades que les exijan poner en marcha sus competencias, en perspectiva de lo anterior, la Evaluación de la Dimensión Teórica (EDT) es descrita por los docentes como la elaboración de instrumentos de evaluación en la fundamentación conceptual de la matemática, para así determinar la base teórica del estudiantado.

A continuación, la Evaluación de la Dimensión Valorativa (EDV) permite la visión del estudiante en su contexto, debido a que se aproxima “en mayor medida a la realidad del acto evaluativo y de los fenómenos implicados en él (…), y de la formación de juicios valorativos, cuyo reconocimiento es imprescindible para lograr una mayor objetividad en la práctica de la evaluación” (Gonzáles, 2001, p.97).

La Evaluación en el Proceso de Desarrollo de Aptitudes (EPDA) manifiesta una deficiencia por parte de los docentes, debido a que no formulan con eficacia fundamentos didácticos, metodológicos y psicológicos que estimulen el desarrollo de actitudes matemáticas como eje principal del proceso de aprendizaje; igual pasa con la Evaluación del Proceso del Rendimiento (EPR), su baja prevalencia describe una disminución en el procedimiento sistemático y estructural para medir los resultados de las competencias matemáticas, con el fin de descubrir en qué medida el aprendizaje es real y efectivo.

En síntesis, los docentes, se caracterizaron por describir una perspectiva evaluativa como un proceso sistemático, esto significa que la evaluación que ellos realizan requiere fortalecer sus procesos y enfoques para el uso adecuado del aprendizaje que mide el mismo proceso, dando coherencia a lo esperado con las acciones emprendidas por las competencias de matemáticas, este aspecto es confirmado por Agudelo y Aldana (2016), los cuales afirman que:

 

en cuanto a la perspectiva de las competencias, el enfoque (…) se hace presente en las acciones evaluativas y hay una conciencia del mismo por parte del grupo de profesores. No se pretende suprimir el uso de este enfoque, pero se hace necesario señalar que los elementos metodológicos, participativos y personales, complementan la noción de este concepto y se pueden incorporar en el proceso de evaluación como consecuencia del favorecimiento de ambientes de aprendizaje y diseños evaluativos diversos orientados a competencias específicas. (83.p)

Por último, las concepciones de las competencias matemáticas en los contenidos curriculares (CPMCC), sí presentan una diferencia importante, en el Aprendizaje Significativo Socio Cultural (ASSC), el cual hace referencia a la interpretación de contenidos y solución de problemas matemáticos ejemplarizándolos en sucesos de la vida diaria o imaginarios en un contexto interesante para los estudiantes. Según López (2002), “la influencia del medio social tiene retos gigantescos en el aprendizaje significativo de las matemáticas (…), comprender que la esencia del niño, no es un ego separado de todo este proceso, aquí su aprendizaje ya es social” (p.3).

La Transferencia de Conocimientos (TC) deben aplicarse en el desempeño en la vida diaria, es así, que los docentes trabajan a partir de los contenidos curriculares referentes a definiciones y ejercicios matemáticos (Gómez y Guzmán, 2013). En este mismo sentido, el Dominio Conceptual Disciplinar (DCD) presente en la muestra ayuda a la construcción de un aprendizaje significativo. Los docentes manejan el saber del área que se quiere transmitir a los estudiantes, para esto el docente realiza una descripción general de la información por medio de la Enseñanza

(E) y el Aprendizaje en relación a la cognición (AC), lo cual se ve reflejado en las acciones dirigidas a desarrollar la participación activa del estudiante a lograr sus metas, con la ayuda de la orientación en la secuencia y orden de los ejercicios matemáticos estructurados para tal fin (Cabanes, et. al., 2017).

Conclusiones

Según los resultados, el enfoque didáctico aplica recursos y metodologías en el desarrollo de las clases al permitir comprender la forma en que los estudiantes razonan y contextualizan en común la variabilidad de formas de solucionar problemas, en sí, la función del maestro es encaminar la apropiación del aprendizaje en el uso de técnicas y razonamientos más eficaces, esto permitirá a su vez, transformar la visión ideal de los sistemas educativos, debido a que existe la necesidad de implementar como eje central el estudio del paradigma educativo para que la comunidad académica se constituya como una sociedad intercultural donde se dé un proceso sostenido, permanente y dinámico de relación, aprendizaje y comunicación mutua.

En cuanto a la Evaluación del trabajo en clase y resolución de ejercicios y problemas matemáticos, permite orientar perspectivas y desarrollar aspectos generales de las competencias matemáticas. Es así como se mantienen las características evaluativas asociadas a la medición del aprendizaje que a su vez puede originar en una proporción desmedida juicios de valor y procesos sistemáticos, que en gran medida también se puede describir como una necesidad educativa, compuesta de una variedad de definiciones y enfoques psicológicos, sociales y culturales, estrechamente involucrados con la motivación de aprender, al mismo tiempo permite demostrar que las Competencias Matemáticas pueden obtener un principio del aprendizaje dialógico, ya que puede llegar a cambiar la forma en que los estudiantes ven los problemas matemáticos, ya no como una forma de adquirir conocimiento especifico, sino como el reconocimiento del ser.

Las concepciones de las competencias matemáticas en cuanto a los contenidos curriculares, determinaron la construcción de un pensamiento numérico, métrico, espacial, aleatorio y variacional, debido a que los docentes facilitan la aplicación de estos pensamientos en un sentido matemático, pero con más relevancia en un Aprendizaje Significativo Socio Cultural (ASSC), el cual contextualiza los contenidos en la solución de problemas matemáticos en sucesos de la vida diaria. Este aspecto de igual manera, permite abordar la interculturalidad dentro de una forma de aprendizaje, en un contexto de educación intercultural la cual debe formar a los estudiantes de todos los grupos culturales hacia la adaptabilidad y desenvolvimiento dentro de un contexto cultural definido. De igual forma las áreas que se debe fortalecer para hacer una sociedad intercultural, están relacionadas con la educación, la comunidad educativa, los docentes y los padres de familia, pues son preciosamente estos grupos los que componen los ejes de la sociedad moderna.

 

 

Referentes bibliográficos

Agudelo, C y Aldana, M. (2016). Evaluación en matemáticas. Una propuesta basada en competencias para el colegio de bachillerato patria (Tesis de Maestría). Universidad Libre, Bogotá, Colombia.

Becerra, J. (2017). Concepciones sobre competencias matemáticas en profesores de educación básica, media y superior. Revista Boletín Redipe [Revista electrónica], 6 (2), 104 – 116. https://revista.redipe.org/index. php/1/article/view/199

Brosseau, G. (2007). Iniciación al estudio de la teoría de las situaciones didácticas. Buenos Aires: Editorial Zorzal. Traducción de: Fregona, Dilma

Cabanes, L., Colunga, S. y García, J. (2017). La matemática en el desarrollo cognitivo y metacognitivo del escolar primario. Edusol [Revista electrónica], 17(60), 45-59. http://edusol.cug.co.cu/index.php/EduSol/article/ view/796

Castela, C. (2017). La teoría antropológica de lo didáctico: Herramientas para las ciencias de la educación. Revista Acta Herediana, 59, 8-15. DOI: https://doi.org/10.20453/ah.v59i0.3052

Castro,C.(2011).Losnuevosparadigmasparalosprocesosdeenseñanza/aprendizajeenlasociedaddelconocimiento en E/LE. Magriberia, (4), 105-116. https://dialnet.unirioja.es/servlet/articulo?codigo=3897595

Chevallard, Y. (1999). El análisis de las prácticas docentes en la teoría antropológica de lo didáctico. España. Recherches en Didactique des Mathématiques. 19(2), 221-266. Recuperado de http://www.ing.unp.edu. ar/asignaturas/algebra/chavallard_tad.pdf

Dane (2018). Registro de la planta docente del departamento de Caquetá. Dane

Diaz, J., Navarro, E., Pacheco, C., Sarmiento, S., Torres, C y Villanueva De Moya, M. (2003). Procesos de evaluación del aprendizaje en el área de matemáticas. Asociación colombiana de matemática educativa Asocolme. http://funes.uniandes.edu.co/955/1/24Taller.pdf

Freudentha, H. (1983). Fenomenología didáctica de las estructuras matemáticas. Herder.

Gómez, A y Guzmán, Y. (2013). La transferencia del aprendizaje en matemática: el caso de las funciones lineal, cuadrática y exponencial. Revista U.D.C.A Actualidad y Divulgación Científica, 16(2), 543-551. https:// revistas.udca.edu.co/index.php/ruadc/article/view/931

Gonzáles, M. (2001). La evaluación del aprendizaje: tendencias y reflexión crítica. Revista Cubana de Educación Superior, 15(1), 85-96. http://sgpwe.izt.uam.mx/files/users/virtuami/file/ext/gestion_evaluacion_actv_ ext_evaluacionaprendizajetendencias.pdf

González, F. (2008). Los límites de la competencia. El conocimiento, la educación superior y la sociedad. Investigación Bibliotecología: archivonomía, bibliotecología e información, 22 (46), 229-235. DOI: http:// dx.doi.org/10.22201/iibi.0187358xp.2008.46.16948.

Grasso, P. (2020). Rendimiento académico: un recorrido conceptual que aproxima a una definición unificada para el ámbito superior. Revista de Educación, 0(20), 89-104. Recuperado de https://fh.mdp.edu.ar/revistas/ index.php/r_educ/article/view/4165/4128

Gregorio, J. (2002). El constructivismo y las matemáticas. Sigma: Revista de matemáticas = Matematika aldizkaria. (21), 113-129. Recuperado de http://www.hezkuntza.ejgv.euskadi.eus/r43-573/es/contenidos/ informacion/dia6_sigma/es_sigma/adjuntos/sigma_21/7_el_constructivismo.pdf

Listón, D y Zeichner, K. (1993). Formación del profesorado y condiciones sociales de la escolarización. Morata.

Ott, R., Longnecker, M., y Tovar, A. (2019). An Introduction to Statistical Methods and Data Analysis. Cengage Learning.

López, M. (2002). El aprendizaje significativo de las matemáticas en tercer grado de educación primaria (Tesis de Pregrado). Universidad Pedagógica Nacional, Cuetzalan, México. http://200.23.113.51/pdf/22135.pdf

Mello, J. (2017). El enfoque de competencias en el currículo de Matemáticas de la Educación Media. La perspectiva docente sobre su implementación. Revista Internacional de Investigación de Ciencias Sociales. 13(1), 14-24. http://revistacientifica.uaa.edu.py/index.php/riics/article/view/352/pdf

Méndez, G., Arboleda, H., Falla, J., Jaramillo, J y Vargas, C. (2018). Paz, tolerancia y cooperativismo a través de las matemáticas en niños y niñas de Caquetá (Colombia). Universidad de la Amazonia.

Moreno, M y Azcarate, C. (2003). Concepciones y creencias de los profesores universitarios de matemáticas acerca de la enseñanza de las ecuaciones diferenciales. Enseñanza de las Ciencias: Revista de investigación y experiencias didácticas, 21(2), 265-280. https://ddd.uab.cat/record/1604?ln=ca

Nieto, L., Mejía, J., Rojas, G., Artunduaga, L., Villegas, P., Escobar, J., Guana, Y y Fernández, H. (2003). Manual de la evaluación de desempeño. Recuperado de https://www.mineducacion.gov.co/1621/articles-81030_ archivo_pdf.pdf

Pareja, F. y Martínez, I. (2008). Concepciones sobre competencias matemáticas en docentes de educación básica, media y universitaria. Revista Boletín Redipe [Revista electrónica], 6(2), 104-118. https://ciencia.lasalle. edu.co/cgi/viewcontent.cgi?article=1575&context=maest_docencia

Peña, D y Prieto, F. (2005). Estadística para las ciencias del comportamiento: con SPSS. McGraw-Hill.

Prieto, M y Contreras, G. (2008). Las concepciones que orientan las practicas evaluativas de los profesores: un problema a develar. Revistas Electrónicas UACh: Estudios Pedagógicos, 34(2), 245-262. Recuperado de http://revistas.uach.cl/index.php/estped/article/view/3317

Puig, L. (2014). Análisis Fenomenológico. Universidad de València. Recuperado de https://cursa.ihmc.us/rid=1HW6T604L-1TJ€€5R0-1RNJ/Ensayo%20acerca%20del%20Analisis%20Fenomenologico.pdf

Radford, L. (2013). Phenomenology, Praxis, and the Question of Mathematical Objects. Educación matemática, 26(Especial 24 años), 124-145. https://www.revista-educacion-matematica.org.mx/revista/2016/08/04/ phenomenology-praxis-and-the-question-of-mathematical-objects/

Ramírez, A. (2016). Perspectiva del nivel educativo de la educación media en Colombia. Paidós.

Resnick, L. (1996). Cognición y aprendizaje. Anuario de psicología, (69). http://revistes.ub.edu/index.php/ Anuario-psicologia/article/view/9097/11610

Serrano de Moreno, S. (2002). La evaluación del aprendizaje: dimensiones y practicas innovadoras. Educere, 6(19), 247-257. http://www.saber.ula.ve/handle/123456789/19715

Socas, M. (2012). El Análisis del Contenido Matemático en el Enfoque Lógico Semiótico (ELOS). Aplicaciones a la Investigación y al Desarrollo Curricular en Didáctica de la Matemática. Valencia. https://core.ac.uk/ download/pdf/33252029.pdf

Tamayo, M. (2004). El proceso de la investigación científica. Limusa.

Van Dalen, D y Meyer, W. (2006). Manual de técnica de la investigación educacional. Paidos Ibérica.

Waldegg, G. (1998). Principios constructivistas para la Educación Matemática. Revista EMA, 4(1), 16-31. http:// funes.uniandes.edu.co/1085/